Related Rates: it is a topic that strikes fear into the hearts of AP® Calculus students everywhere. Why is this topic so challenging for first year calculus students and what can be done to help them through it? Here we will look at an idea that can go a long way in helping students prepare to tackle related rates problems.First, remember this: All Math is the Same – Students like to pretend that they can’t do a math problem because they have “never seen one like it before.” The beauty of math is that it always works perfectly if used consistently. In almost every related rate example a student is asked to find something. How many times has a high school student been asked to find an unknown in a math class? Countless times students are asked to find x or some other variable and they learn to do so without even thinking about it. If you ask a Calculus student to find the missing leg of a right triangle given that one of the legs is 4 inches and the hypotenuse is 6 inches very few would struggle. However if you ask that same student to solve the following:

“An inverted (point down) right conical tank with a height of 12 inches and a radius of 4 inches filled with water is draining at the rate of 5 in³ /second. Find the rate of change of the height of the water in the tank when the height is 3 inches.”

They will tell you these two problems are completely different. This is the paradigm that needs to change. Not only are these two examples very alike, in many ways they are exactly the same.

Let’s look more deeply at these two examples and explore the similarities. In the case of the right triangle students identify the unknown they are looking for very quickly as the leg of a right triangle. They also identify the other given information, in this case the hypotenuse and the other leg of the triangle. Many students will draw a picture (if helpful) to help them organize the information.

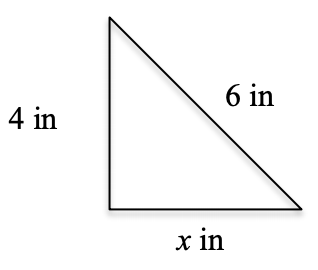
Now the key will be to find an equation that relates all of the given material, especially one that contains the hypotenuse of a right triangle since that is what we are being asked to find. It doesn’t take long to come up with the Pythagorean theorem,

a² + b² = c²

Using the given information we can now substitute this information and the only unknown left will be the leg of the triangle, which is precisely the quantity we were asked to solve for.

What were the steps we followed to arrive at our answer?

1)

identify the unknown
b – The missing leg of the right triangle

2)

identify the other given information
c – The hypotenuse = 6 inches
a – The leg = 4 inches

3)

draw a picture (if helpful)

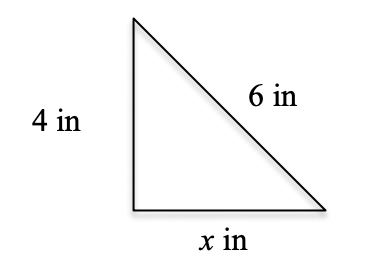
4)

find an equation that relates the unknown we are after with ONLY the given information
a² + b² = c²

5)

substitute
4² + b² = 6²

6)

solve
4² + b² = 6²
16 + b² = 36
b² = 20
b = √ 20 

Therefore the missing leg is √ 20  inches long.

Now let’s look at the related rate example:

“An inverted (point down) right conical tank with a height of 12 inches and a radius of 4 inches filled with water is draining at the rate of 5 in³/second . Find the rate of change of the height of the water in the tank when the water is 3 inches deep.”

Right away, students are not as comfortable with this and will say it is a far more difficult problem. In order to combat this, students must really decipher what is asked and translate each part to the language of mathematics.

For instance:

The word “rate” implies that something is changing and therefore we need a derivative. Read the sentence to find out what is changing…

rate of change of the height

Now we know the height is changing with respect to time and to denote that mathematically we write rate of change as ^{d[ ]}⁄_dt. Since the height is changing we use ^dh⁄_dt.

1)

identify the unknown

^dh⁄_dt – the rate of change of the height

2)

identify the other given information

^dV⁄_dt – The rate of change of the volume = -5 in³/second (water is leaving the cone)
h – The height of the water = 3 inches (Be careful, this is only true when finding the answer)
Height of the cone is 12 inches (always true)
Radius of the cone is 4 inches (always true)

3)

draw a picture (if helpful)

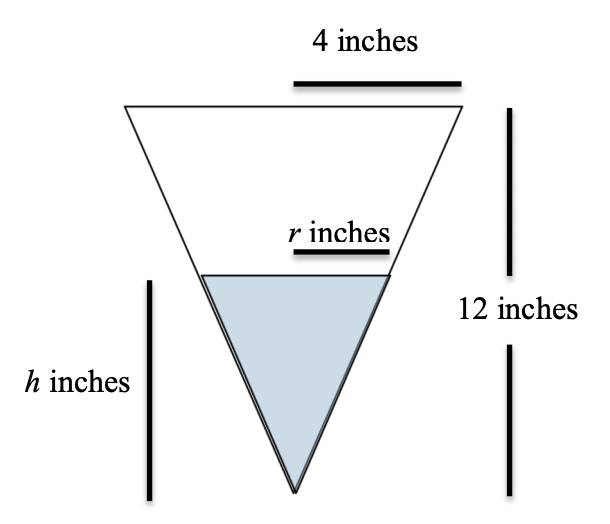
4)

find an equation that relates the unknown we are after with ONLY the given information

Here is where the trouble begins for our calculus students. It is straightforward to realize we need an equation with ^dh⁄_dt since that is the unknown we are looking for. The problem most students will have is even though they know what we want in our equation, most do not know any equations that contain a ^dh⁄_dt.

So, what is the next best thing to an equation with ^dh⁄_dt in it? It is an equation with h. As long as we know an equation with h we can create an equation with ^dh⁄_dt by taking the derivative. Now this comes down to finding an equation with the height of a cone present keeping in mind that we have knowledge of the volume of the cone as well. This makes the choice of equations:

V = ¹⁄₃ π r²h

We like this equation since it has an h in it and a V in it. When we differentiate with respect to time it will result in ^dh⁄_dt and ^dV⁄_dt in our new equation and we are fine with that. Unfortunately, since there is an r in the equation we will also have a ^dr⁄_dt in our equation after differentiating, but we have no information about ^dr⁄_dt, so that is not desirable. One way to fix this is to see if we can replace the r with either h or V. In order to do this we will have to find a new equation with r relating it to either h or V. This is where practicing old AP exam questions comes in handy. There are several old AP questions that deal with conical tanks (and shadows); samples include the 1991 (AB exam, problem 6), 1995 (AB exam, problem 5) and 2002 (AB exam, problem 5) AP Calculus exams. All of these problems illustrate the use of similar triangle to replace a variable. Remember our picture:

^r⁄₄ = ^h⁄₁₂ so r = ^h⁄₃ and using that

V = ¹⁄₃ π r²h becomes V = ¹⁄₂₇ π h³

Differentiating both sides of V = ¹⁄₂₇ π h³ yields

^dV⁄_dt = ¹⁄₉ π h² ^dh⁄_dt

and we now have the equation that relates the unknown we are after with only the given information. Now,

5)

substitute

-5 = ¹⁄₉ π (3)² ^dh⁄_dt

6)

solve

-5 = π ^dh⁄_dt

^dh⁄_dt = – ⁵⁄_π so the height of the water is changing at a rate of – ⁵⁄_π when the height is 3 inches, which means the height is decreasing at a rate of ⁵⁄_π inches/second.

I will agree that this related rate problem had the added difficulty of getting an equation with only the information we were given (i.e. we had to replace r) but the approach was the same as the Pythagorean theorem question. Students should not say they do not know how to do this problem! They might say I do not know how to get an equation with ^dh⁄_dt but that is a very different level of understanding.

What makes mathematics so beautiful to me is the idea that, as we said above, All Math is the Same. “Find” always means the same thing whether we see it in an 8^th grade algebra class or in college level calculus. Knowing how to approach a problem is a huge part of your success!