Last year at around this time, we posted a blog about physics concepts that you needed to know as you got through the first month or so of the course, titled “Physics Concepts From the Beginning of the Year that you Simply Must Know”. We reviewed topics students typically had difficulty with, that they were sure to see again, and which formed the basis for much of the rest of the course. Chemistry is slightly more disjointed, and there are concepts students will encounter later in the semester such as quantum mechanics that will have nothing to do with the first few weeks. Still, some areas do come up as problems regularly, and if they are addressed early on, it will make life way easier going forward. Here we will look at a couple of those themes: stoichiometry, which comes up frequently during the year, and limiting reagents, which appears less frequently but seems to cause problems whenever it does.
The first couple of weeks of an AP® Chemistry course are generally a review of stoichiometry, which involves lots of dimensional analysis of basic equations. Stoichiometry is derived from the Greek words “stoicheion” (element) and “metron” (measure), and is a quantitative analysis of chemical reactions and formulae. Simply put, this comes down to multiplying and dividing ratios of one dimension to another. For some of you this will seem very simplistic, but there are many kids enrolled in AP Chemistry at some pretty top tier schools who struggle with this, so it may be worth your while to review. Let’s begin with a non-chemistry example: how would you answer the question,
“How many seconds are in one year?”
Most students would begin by writing 60/min, 365/year etc. etc. and would eventually get it after a while. But there are systematic approaches to this problem that will insure you don’t make mistakes.
Let’s begin by looking at what the question asks for; it is asking for some number of seconds as a final answer. So, how to begin? You start by writing “= ______ seconds”, towards the right of the space you are working in, as below. Then ask yourself, what are you given to start with? You are given one year. So you take what you are given and write that on the left, followed by a bunch of brackets which you will use for conversion factors:

Now, how many conversion factors will you need? In advance, you won’t know. But as you work through the problem, it will become obvious. Now on the bottom of the first bracket, put in the word “year”, or whatever is the unit you start with. The number of years won’t matter; you just want the units to match.
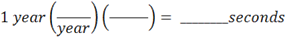
And on the top of the last conversion factor, write in “seconds”, or whatever the unit is you are asked to find:

Once you do this, the approach becomes clearer, as you have sketched the outline of the problem. You are starting with the given units on the left, and will work towards the requested units on the right, filling in the conversion brackets along the way. Now, what you must do is INCLUDE THE UNITS AS YOU WORK THROUGH EACH CONVERSION FACTOR. This way, you will know you have done the problem correctly if the units cancel, and you end up with the units you are asked for!
So, our solution will look like:
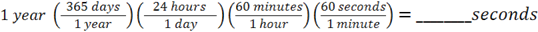
A couple of details: First, make sure you write your conversion factors like this,
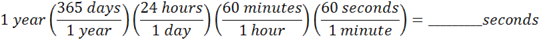
because it is much easier to see if your units cancel. If you draw them like this,
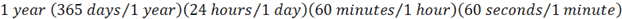
then it is less obvious to if the units cancel.
Second, although most of these problems contain 3 or fewer conversion factors, it is perfectly legit to break them into smaller bites…that is, you can do the problem as such, which some students seem to prefer:
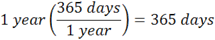
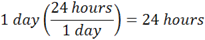 etc.
etc.
Let’s look at an actual chemistry problem: “How many gms of water are produced in the combustion of one gram of glucose?
In this, as in many stochiometric problems, we work from a balanced equation:
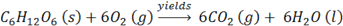
We begin by writing “= ___________ gms H2O ” on the right, and “1 gm of glucose” on the left followed by several conversion factors, i.e.
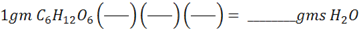
As before, you draw in gms C6H12O6 on the bottom of the first bracket, and gms H2O on the top of the last bracket. The problem will then almost do itself, because the outline is there in front of you.
Limiting reagent problems are another type of problem that students often struggle with. In a limiting reagent problem, you have to decide which reactant runs out first, how much product you produce, and how much of the excess reactant remains at the end of the reaction. Again, you have to start with a balanced equation, but the approach is really somewhat flexible; just remember that you are working initially with the left side if the equation. Say the problem is based on the reaction:
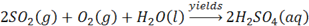
and asks how much H2SO4 can be formed from 4.0 moles of SO2, 1 mole of O2, and an unlimited amount of H2O?
What many students don’t get is that you can start with either reactant, so long as you use JUST the reactants in your conversion factor, and you will get the same information. So if you start with 4 moles of SO2
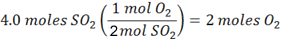
We see that 2 moles of O2 are required, and since we only have one, we know right away that O2 is the limiting reactant. And, therefore, that SO2 is the excess reactant.
Conversely, we can begin with 1.0 mole of O2
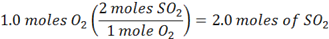
and since we have 4.0 moles of SO2, we know SO2 is the excess reagent. As such, O2 is the limiting reagent, so we get the same
information from doing this either way. Once we know the limiting reagent, we figure out from there how much product (in this case H2SO4) we derive if we begin with 1.0 moles of the L.R. (in this case O2).
As for how much remains after the reaction, we have more SO2 than we need, and the amount that is not used during the reaction (4.0 moles available – 2.0 moles used) will give us what we have left over after the reaction runs to completion.
Remember,the way you learn how to do these and all other types of problems is just by…doing lots of problems! Don’t be discouraged when you get them wrong, they just take practice. Amongst the best problems to try are the worked problems from your textbook, because you can look at the problem, cover up the solution, and compare the way you worked the problem with how the book does the problem. Doing as many of those as possible will help your understanding tremendously!
Good luck! Be sure to give us a shout if you have any questions.
AP® is a trademark registered and/or owned by the College Board, which was not involved in the production of, and does not endorse, Warp Drive Tutors.
