This test is no longer offered

Written by Joel

To begin, take a diagnostic test: About 8 weeks before the test, you will want to take the first SAT Math Level 2 practice test found on page 119 of “The Official SAT Subject Tests in Mathematics Level 1 & 2”, published by the College Board®. Allot yourself exactly one hour, with a timer. It is very important you not go over the allotted time, (unless you get time and a half) to assess where you are and how to best design a plan going forward. Please note this is a real test, and as such serves as an excellent benchmark to determine where you are currently. Note: Do NOT take this until you are at least 8 weeks away from the end of your math course, because your class will still need to cover a fair amount of material. If you take the test much earlier, it will be tough to determine what you don’t understand vs what you just haven’t yet learned in your course. This does not imply you can’t begin prepping earlier – remember, the test is based on your entire course, so if there is material from the Fall you still don’t get, the earlier you begin review the better.

Essential Facts You Need To Know Before Getting Started

•LENGTH: The test consists of 1 section of 50 questions for which you have 60 minutes.

•QUESTION FORMAT: A – E multiple choice.

•MATERIAL COVERED: The recommended prior coursework is the same as Math Level 1 except with the addition of trigonometry and pre-calculus.

•TOPICS INCLUDED: See page 21 of “The Official SAT Subject Tests in Mathematics Level 1 & 2”, published by the College Board. This gives a complete breakdown of topics by percent, and you should definitely READ THIS CAREFULLY, and circle ALL areas where you feel you are weak.

•Most questions can be answered without a calculator, but use of one is expected for certain calculations. Scientific graphing calculators are allowed.

Taking The Test Soon After The General SAT®: For a long time, the “go to” advice was to take this test as soon after taking the SAT as you can, because all of the math specific techniques you learned for that test are applicable here as well. However, since the SAT has moved to a 4 answer per question format, the strategies are no longer so closely aligned, and you need not think of taking the Math 2 Subject test with any regard to your schedule for the general SAT. Incidentally, the same goes for the ACT: the question types and strategies for the math section are different than what we will concentrate on here.

General Strategies: We are going to examine some general test strategies and then focus in on some question specific strategies with examples.

General Strategy 1: Think Process of Elimination (POE) Think about each question you see in terms of process of elimination. Do not try to determine what the answer is; rather, ask yourself what the answer is not. Why is this? Because for a large percentage of the test, you will have to take your best guess at the correct answer. Since the answer is in front of you, there is a statistical likelihood that you will guess correctly by eliminating at least one of the answers. Let’s examine that statistical likelihood.

For example, suppose you have 10 questions, each with answers A-E. The College Board gives you plus one point for each correct answer, minus 0.25 points for each incorrect answer, and no points for any answers left blank. Let’s say you eliminate one answer that you know is wrong from all ten questions, and for the sake of argument say this is “E”. Now, you guess randomly from the remaining 4 answer choices, A through D. Statistically you will guess correctly one time out of four. How many points will this get you?

2.5 Correct = 2.5 points x +1 point =    +2.5 points
7.5 Wrong = 7.5 points x -1/4 points = -1.9 points
You Score                                                               +0.6 points  

This is enough to raise your score from a 690 to a 700.

Therefore, Always guess if you can eliminate one answer. NEVER GUESS if you CANNOT ELIMINATE AT LEAST one answer. For example, what is the graph of the equation

(A) a circle
(B) an ellipse
(C) a hyperbola
(D) a parabola
(E) two straight lines

You should probably be able to cross out (E). Once you do, guess from the remaining 4! Your statistical benefit from guessing outweighs the possible penalty. Incidentally, the correct answer is (C).

General Strategy 2: Know how the order of questions pertains to the difficulty of the question:  Let’s review how the Math Level 2 Subject Test is structured in terms of question difficulty. The first thing to realize is the increasing order of difficulty as the questions progress. The beginning questions are “easy” and they get more difficult as you go from questions 1-50. This is never exact, but one can assume the first third are “easy”, the second third “medium”, and the last third are “difficult”.

That is,

Approximate question number                 Difficulty level

1 – 17                                                                         Easy

18 – 35                                                                      Medium

36 – 50                                                                      Difficult

What do we really mean though, by “difficult”? It is important to define the concept of “difficult”, as far as the SAT tests are concerned. A difficult question is not necessarily a question that asks you something conceptually challenging. Rather, a “difficult” question is a question that the majority of students answer incorrectly. That is, for a difficult question, the answer choice that looks like the correct answer almost never is, but because most people pick that as the answer, it is answered incorrectly much more frequently. So on the difficult parts of the test, if you find yourself answering the question with the answer choice that “looks” correct, you must recognize that it in fact is almost never correct. Put differently, the more difficult the question, the more likely there will be several traps. Paying attention to the order of difficulty, and where the question lies in the sequence, will help you determine when to go with your gut and when to eliminate answers that feel “too easy.”

Why is it necessary to discuss this? First, it is always to your advantage to tackle the easier problems on a test before going to the tougher ones, and this goes for your non-standardized tests as well. But more importantly, these tests are curved, and the curve is somewhat predictable. That is, you need not answer all the questions to get a high score. Further, you score the same number of points for each correct answer regardless of whether that question is easy or difficult. Question 1 gets +1 point, as does question 48. Likewise, an incorrect answer receives –1/4 point, no matter the location of the error. Thus, it makes sense to omit certain questions if you absolutely can’t answer them (ie cannot eliminate one answer choice), if you don’t need to answer all of them to get a high score. Since you receive the same +1 points for each correct answer regardless of where you answer the questions, the questions you choose to omit should come from the more difficult sections. You need not answer all of the questions in order to get a high score.

So, what is the curve? For the Math Level 2 test, it is fairly reproducible that you will score a 700 if you answer 70% of the test correctly, while omitting the remaining questions – ie, just leaving those questions blank. This means you can answer 35 questions from a 50 question test correctly, without making any mistakes, and get a 700. In theory, you can omit nearly a third of the test. Which part of the test would you omit? The more difficult part, or questions 36-50. Of course, you are probably not going to get every one of those questions in the first 70% of the test correctly, but the point is that when you are going to omit answers – and you can – you should try to save the blanks for the most difficult, later portion of the test.

Now, however lets go back to our original statement: ALWAYS GUESS IF YOU CAN ELIMINATE ONE ANSWER CHOICE. Always guess if you can eliminate one answer choice. NEVER GUESS if you CANNOT ELIMINATE AT LEAST one answer choice. Even considering the curves, the statistics are in your favor if you guess when you can eliminate one answer. Your score WILL go up.

Question Strategies: 

1) The single most important strategy you will use is “backsolving”, which is a valuable technique when all of the answer choices are numerical, and the question asks you for the value of a single variable. This technique is not useful if the question does not ask to solve for a variable, or it asks to solve for more than one variable. So, if the answers are numerical, AND you are asked for the value of a single variable, look at the answers, take the intermediate value, and plug this into the equation. Do not try and solve the equation, the answer is in front of you. See if the intermediate value works, and proceed from there. Is the value too small? Try answers D and E; if the answer is too large, try answers A or B.

Do not feel that you absolutely MUST use this strategy, as solving the problem mathematically will sometimes prove the faster option. But backsolving is the first thing you should consider when you see answer choices with numerical values.

Let’s try the backsolving technique with a few problems:

Example 1: In the function

what is closest to

(A) 1.4
(B) 1.5
(C) 2.0
(D) 2.3
(E) 2.5

Plug in answer choice (C). Notice that the value you get is too small; this means you must move down to answer choices (A) and (B). The correct answer choice is (A).

Example 2: Derek deposits $5000 into a new savings account that earns 8% percent interest compounded continuously. If Derek makes no additional deposits or withdrawals, how many years will it take for the amount in the account to triple according to the formula P=Pe?

(A)14
(B)15
(C)19
(D)20
(E)21

Plug in answer choice (C). The value is too big, so move up the answer choices until you get to answer choice (A).

2) The second most important strategy to use: insert an integer or a number when the answer choices are variables.

Example 1: For all angles theta,

?

So say plug in zero for and the answer of will be obvious.

Example 2: For some real number p, the first three terms of an arithmetic sequence are

What is the numerical value of the fourth term?

(A)5
(B)9
(C)11
(D)17
(E)19

Does it really matter what p is? Do we need to remember the formula for calculating the difference between terms of an arithmetic sequence?

The College Board likes to create problems that have shortcuts. Sometimes you may find yourself thinking deeply about a formula when the College Board is trying to gauge your understanding of WHAT an arithmetic sequence is; it’s likely that there’s a shortcut you are missing…more on that later. For now, plug in 0, 1, or 2. You will see that 2 works!

Example 3: Which of the following equations best models the data in the table below?

(A) y = -3.3(1.4)
(B) y = -1.4(3.3)
(C) y =  1.4(3.3)
(D) y =  3.3(1.4)
(E) y =  1.4

And combining this with the I, II, III type questions we saw before,

Example 3: All of the following are ways to measure the central tendency of a set of data EXCEPT

I. mean
II. mode
III. standard deviation

(A) I only
(B) III only
(C) I and II only
(D) I and III only
(E) II and III only

Put your thumb on the word EXCEPT. Now if you know that mean is a measure of center, go ahead and cross out every answer choice that has statement I. As a result, you would end up choosing between answer choices (B) and (E).

Example 4: The graph of the function is shown below

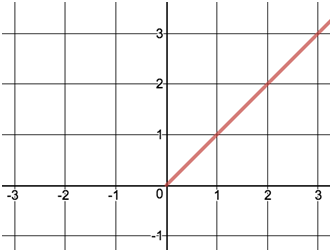
Which of the following CANNOT be the rule of the function?

(A)  f(x) = |x| for x>0
(B)  f(x) = x for x>0
(C)  f(x) = |x+1|-1 for x>0
(D)  f(x) = -|x-4|+4  for x>0
(E)  f(x) = |4-x|-4  for x>0

Put your thumb on the word CANNOT. Go ahead and cross out the answer choices that are true. If you can cross out (A) and (B), then you have a better shot at getting (E).

Remember, no amount of test taking tricks or techniques will help you if you don’t understand your trigonometry; there is no such thing as getting a high score on a test if you don’t know the subject material. Test taking techniques are useful, and much of what you would need to know is encapsulated here, but if you are getting a B -? Forget the Subject Test and concentrate on bringing your course grade up.