Written by Giuseppe

Introductory Physics classes will typically cover three important conservation laws: conservation of energy, conservation of momentum and conservation of angular momentum. In this blog post, we will focus specifically on conservation of energy and on applying it to problems that you will find in your Physics class assessments. Energy conservation is a fundamental tool for understanding an incredible array of natural phenomena, from electron orbitals to lightning, volcanoes, waterfalls and photosynthesis. It also has practical applications to all sorts of everyday applications, including anything that bounces (such as a tennis ball), bungee jumping (where the object is most definitively not to bounce), your toaster, and the weights you lift in the gym. However it is an often misunderstood and misused concept. One of the goals of your Physics class is to give you the tools to understand what energy is and why it is important. A clear definition of energy is not straightforward, but it is useful to begin with a list of properties that help to define what it is, and what it is not. Herein, we list five properties you will need to consider:

1. Energy is a physical quantity of a system which can be calculated from other physical quantities such as mass, volume, velocity, temperature, etc.
   Like all physical quantities, it has a unit of measure which in the SI system is the joule (J). Other frequently used units for energy are the calorie (cal) and its multiple kilocalorie (kcal) and the kilowatt-hour (kWh).
   The kWh is not to be confused with the watt (W) or kilowatt (kW) which are units of power, not energy. It is useful to remember the ratio of calories and kWh to joules:                                                                                                                                                                                                                                                                                                                                                                                                                                                      1 cal = 4.186 J
   1 kWh = 3.6×10⁶ JAnother unit of energy we encounter, especially when dealing with atoms or sub-atomic particles, is the electron volt (eV), where 1 electron volt = 1.6×10⁻¹⁹ J.
2. Energy has different forms
   A physical system can have different types (or forms) of energy and its total energy is obtained simply by adding up the different types of energy; your system might include kinetic energy, several types of potential energy (such as elastic or gravitational), thermal energy and possibly others. It can be useful to introduce an analogy which explains how energy works. Money can exist in different forms in that you can have some money in cash (in banknotes and coins), some money in a bank account, and maybe some in a prepaid credit card or electronic wallet. These are different forms of money, and you get your total money simply by adding up the different amounts you have in the different forms.
3. Energy can be transformed from one form into another
   It is possible to transform or convert one form of energy into another, and it is indeed what happens almost every time an interesting physical phenomenon occurs. For example when something falls, its gravitational potential energy is converted into kinetic energy and, because of friction, into thermal energy, and when a ball bounces its kinetic energy is transformed first into elastic potential energy and then back to kinetic energy. Similarly, you can deposit cash on your bank account, withdraw cash from an ATM or load some money from your bank account onto your prepaid card or electronic wallet, changing the form of your money.
4. Energy can be transferred from one system to another.
   This means that the total amount of the energy of a physical system can increase or decrease because of the increase or decrease in energy of another physical system. So if you place a warm body in contact with a cold body, the energy of the cold body increases because energy is transferred to it from the warm body. The analogy with money still holds; ie, money can pass from one person to another person in an economical transaction. The exchanges of energy, however, are bound by the Law of Conservation of Energy, which states that:
5. The Total Energy of the Universe is Constant.
   What this means is that transformations of energy are limited by its conservation, so if a form of energy of a system decreases by a certain amount, some other form must increase by exactly the same amount. This property of energy must always be taken into account. Even when we speak about energy “production” or “renewable energies”, we must always remember that we are actually dealing with energy transformations from one form into another. Again, the analogy with money can be helpful: when you buy something, your total money decreases by a certain amount, while the vendor’s money increases by that same amount. Despite the fact that we use terms such as energy “transformation” and energy “transmission”, it is fundamental to the understanding of energy conservation that energy is not a physical substance. When energy is “transferred” from one body to another, nothing is physically passing from the first body to the second, and their properties are changing in such a way that the account of total energy is unchanged. Of course, the fact that the total amount of energy in the Universe cannot change doesn’t mean that the energy of a single system must stay unchanged. There are two ways in which the energy of a system can change:
   1. Work
      When a force 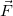acts on a body and its point of application displaces by an amount 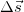the work done by the force 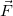is given by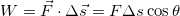
      

      The expression 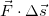is called the scalar product of the two vectors 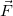and 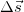and θ is the angle between the two vectors. We note that while work is not a vector, it can have a positive or negative value.

   2. Heat
      Heat (symbol ) is the amount of energy transferred from a warmer body to a colder one.

   Work and heat are the only two ways in which the energy of a system can change. They are both measured in joules and their relation to the change in energy is quite simple: if a force does work W on a system and the same system receives an amount Q of heat, then its energy change ΔE is given by

   

   This equation is the First Law of Thermodynamics.

   Applications to IB® Physics questions:

   1. The first example is taken from the 2014 Specimen Paper 3

   
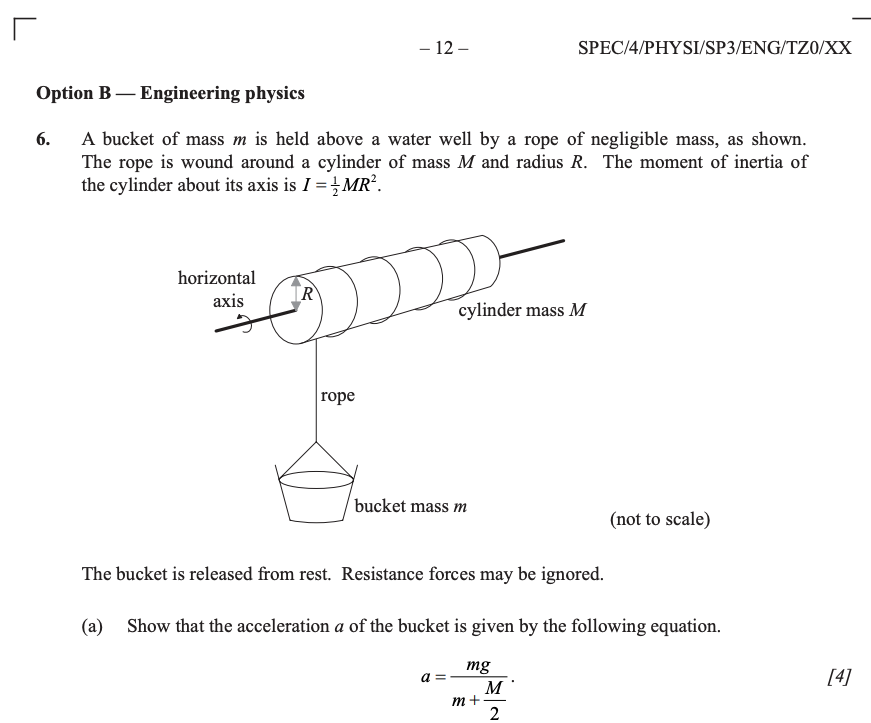
   The proof is easily obtained applying the rules of moments of forces and moments of inertia (it could also be obtained by applying conservation of energy, but it’s not convenient in this particular case).
   

   This is a type of question that is most easily answered using conservation of energy.
   In general, whenever we have information about the state of a system at a certain time and we want to know something about the system at another time, without being interested in how long the process takes or the details of its evolution, conservation laws are the best tools.

   As the bucket falls and the cylinder spins, the total amount of energy of the system is given by the rotational kinetic energy of the cylinder, the kinetic energy of the bucket and the gravitational potential energy of the bucket.

   

   Remembering that and that, in this situation we have

   

   At the beginning, the bucket is at rest at a certain height h_o, while when it has fallen Δh = 16 m it has speed v (the unknown in this question) and its height is clearly  h_o  –  Δh. We can thus write

   

   Solving for gives, with simple algebra

   

   

   Power is the rate of change of energy

   

   As the bucket is lifted at a constant speed, the kinetic energies of the cylinder and the bucket itself are unchanged. In a certain time Δt, the bucket is lifted by Δh = vΔt and the energy change ΔE is given by

   

   from which we can obtain the power output

   

   This increase in energy is caused by the work done by the motor on the cylinder and comes at the expense of the electric energy of the batteries which are supplying the motor.

   2) The following questions regard the transformations between different types of energy and are classic IB examination style questions.

   A stone of mass 0.150 kg is released from rest from the top of a high cliff.  Air resistance is not negligible.  After 8 s, the stone has fallen 160 m and its speed is 21 m/s.
   

   1.  Calculate how much its mechanical energy has decreased (mechanical energy is the sum of kinetic and potential energy). We can easily obtain the result by noticing that, as v_i = 0 and v_f is the final speed, respectively, and h_i  = 0 and h_f  = 0 the initial and final height, the change in energy is given by
   2. 

      The ball is dropped from rest, thus v_i  = 0 and from the graph, v_f  = 25 m/sec from which we obtain

      

      (Notice that here Δh = -160 m because the final height is 160 m less than the initial height).

   The obvious question is now “where has the energy gone?” or, better, “to what form has it changed into?” The answer is that whenever friction is involved, some energy is transformed to thermal energy. Indeed, it is a property of friction to transform mechanical energy (the sum of kinetic and potential energy) into thermal energy. Air resistance is a type of friction and the resulting conversion of mechanical energy into thermal energy is, for example, what makes a shooting star possible! Shooting stars are simply small asteroids that, after having entered Earth’s atmosphere, heat up enough to become bright and burn in the sky. The next questions explores this phenomenon:

   2. The specific heat capacity of the stone is 750 J/kg K. Estimate how much its temperature has increased. As the verb “estimate” suggests, in order to answer this question, we need to make some assumptions. As we have already said, when friction is acting, thermal energy increases. When rubbing two surfaces together, they both heat up because of friction but it’s really hard to tell how much of the generated thermal energy each one receives. We can only state that the total energy remains unchanged. In this case, friction acts in the form of air resistance between the air and the stone and thus:

It seems reasonable that each of the two objects between which friction acts gets roughly 50% of the thermal energy. In this case, we can thus assume, for example, that 50% of the “lost” mechanical energy is converted into thermal energy of the stone, while the remaining 50% is converted into the atmosphere thermal energy.