Written by Marizza; Marizza is available for private tutoring.
Wordymathphobia
Wordymathphobia: (noun) An abnormal or pathological fear of seeing words in your math
Many students seem to be under the impression that word problems are spawned by spiteful math teachers who wish to traumatize them into obedience. At least, that is what some of my students tell me when I ask them why they leave all the word problems blank on their homework. Woefully, word problems are merely the math teacher’s attempt to answer one of the most common student questions:
“When are we ever going to use this stuff, anyway?”
For example, Related Rates word problems reveal how Calculus can be used to calculate the rate of change of a measurement when variables are related to each other. Most word problems are demonstrations of applications of mathematics to various fields in the “Real World”.
Sadly, in the “Real World” people communicate using words, which means you WILL be confronted with a verbal or written problem. In order to solve it, you may need to convert those words into mathematical relationships. In other words, if you want to adult successfully, you are going to have to get over your wordymathphobia and solve those suckers.
Before you run away screaming and hide under your bed, keep reading.
Below is a strategically crafted plan of attack that will help you beat those words into submission, so that you, the victorious student, emerge unscathed with the solution in your hand (or on your paper), and your sanity intact.
Word Problem Strategy:
Step 1: Underline Breathe! Don’t Panic! These are usually words that occur frequently in your math book. Your math teacher usually uses these words repeatedly so that, by osmosis if necessary, you will retain them.

© Illustrated by Sabrina @binathewitch
Step 2: Draw, draw, draw (and label) Still panicking? This will help. Draw a picture modeling the situation in the word problem. This is usually the most helpful and most neglected step. Don’t skip this step! You can use colors if it makes you happy and don’t worry if you’re not Van Gogh.

© Illustrated by Sabrina @binathewitch
Step 3: Name Everything Otherwise known as identifying variables, giving names to what is known and what is unknown is just polite. No one wants to go around shouting “Hey you!”. Identify what is changing (variables) and what is constant. Substitute the constants with their values. Do not substitute the variables with their values until the end.

© Illustrated by Sabrina @binathewitch
Step 4: Determine math expressions from picture and math In order to be able to execute this step correctly (I’m sorry to break this to you), you need to STUDY your math vocabulary. I know! I know! You aren’t used to studying vocabulary and definitions in math. Too bad. Write the expressions and equations you’ve translated from the math vocabulary down on the paper. They don’t do anyone any good hiding in your head.

© Illustrated by Sabrina @binathewitch
Step 5: Determine what you’re asked to find and solve Identify the variable you are asked to find and keep reminding yourself that it’s your goal. Once you’ve written all equations down on, look for connections until you have answered the question. You may need to look back at your picture for extra relationships.

© Illustrated by Sabrina @binathewitch
Let us see how we would use the steps above on a related rates problem found in Thomas’ Calculus book:
Calculus I Example (AP®Calculus AB): (Thomas’ Calculus 11th edition, p 221 #34)

SPOILER ALERT! Solution included below:
Step 1: Underline
All numbers with units should be underlined. The word “decreasing” is often discussed when derivatives are mentioned, and the word “speed” is relevant to derivatives.
Highway Patrol: A highway patrol plane flies 3 miles above a level straight road at a steady 120 miles per hour. The pilot sees an oncoming car and with radar determines that at the instant the line-of-sight distance from plane to car is 5 miles, the line-of-distance is decreasing at the rate of 160 miles per hour. Find the car’s speed along the highway.
Step 2: Draw, draw, draw (and label)
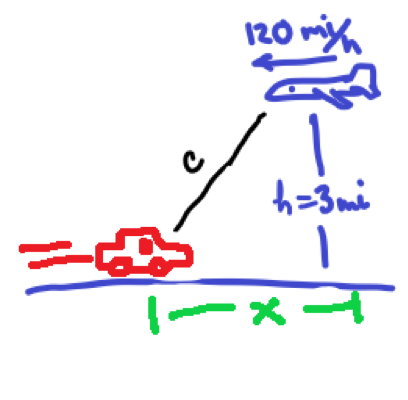
Figure 1: Sad Excuse of a drawing by Marizza
Step 3: Name Everything
- Call the height of the plane, h.
- The height of the plane is not changing so
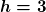 is a constant.
is a constant.
- The height of the plane is not changing so
- The plane is flying a steady
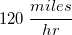
- call the velocity of plane, v, v = 120 mph
- steady implies the velocity of the plane is not changing, v=120 mph is a constant.
- Call the line-of-distance, c.
- “the instant the line-of-sight ( c ) is 5 miles”
- Instant implies c is changing, c is a variable
Step 4: Determine math expressions from picture and math vocabulary
- “the line-of-distance, c, is decreasing at 160 miles per hour”
- The derivative of c is negative,
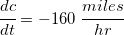
- The derivative of c is negative,
- From the picture, we can see there is a horizontal distance from the car to the plane, x
- x is changing, x is a variable
- From the picture we can see a right triangle with sides length c, h, and x.
- Pythagorean Theorem
- h = 3 is a constant, but c and x are variables
![]()
![]()
-
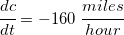 , we need to derive implicitly
, we need to derive implicitly
![]()
![]()
![]()
There are two variables left, x and ![]() .
.
The paragraph does not contain either, however, if we use “at the instant that c = 5”, we will get two sides of a right triangle.
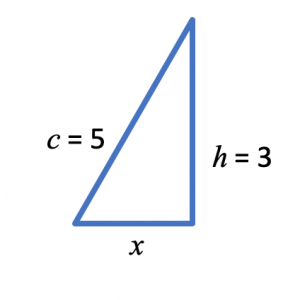
From the Pythagorean Theorem, we can compute that x = 4.
![]()
![]()
![]()
![]()
Step 5: Determine what you’re asked to find and Solve
The question at the end of the paragraph is “Find the car’s speed”.
The speed of the car is not ![]() because x is measuring the position of the car relative to the plane, which is going in the opposite direction.
because x is measuring the position of the car relative to the plane, which is going in the opposite direction.
Therefore, we need to subtract the plane’s velocity from the ![]() in order to get the car’s speed:
in order to get the car’s speed:
![]() miles per hour
miles per hour
The End
The solution seems much longer only because explanations were inserted.
Now, let’s try this again without all the explanation with part (b) of the AP Calculus AB/BC Free Response question from 2018.
2018 AP® Calculus BC Free-Response Questions
2. Researchers on a boat are investigating plankton cells in a sea. At a depth of h meters, the density of plankton cells, in millions of cells per cubic meters, is modeled by p(h) = 0.02h²e-00025h² for 0 < h < 30 and is modeled by f (h) for h > 30. The continuous function f is not explicitly given.
b) Consider a vertical column of water in this sea with horizontal cross sections of constant area 3 square meters. To the nearest million, how many plankton cells are in this column of water between h = 0 and h = 30 meters?
Try it on your own first, then look at the solution below! ( Don’t peek. )
Step 1: Underline and Highlight
Step 2: Draw, draw, draw (and label)
Step 3: Name Everything
Step 4: Determine math expressions from picture and math vocabulary
Step 5: Determine what you’re asked to find and solve
SPOILER ALERT! Solution included below:
Step 1: Underline and Highlight Do you see any vocabulary words? Also, anything with units gives us information about whether we’re dealing with a derivative or not.
2018 AP® Calculus BC Free-Response Questions
2. Researchers on a boat are investigating plankton cells in a sea. At a depth of h meters, the density of plankton cells, in millions of cells per cubic meters, is modeled by p(h) = 0.02h²e-00025h² for 0 < h < 30 and is modeled by f (h) for h > 30. The continuous function f is not explicitly given.
b) Consider a vertical column of water in this sea with horizontal cross sections of constant area 3 square meters. To the nearest million, how many plankton cells are in this column of water between h = 0 and h = 30 meters?
Step 2: Draw draw, draw (and label) We may not need to draw the researchers, but we could draw the boat, and should draw the sea and the vertical column of water with horizontal cross-sections.
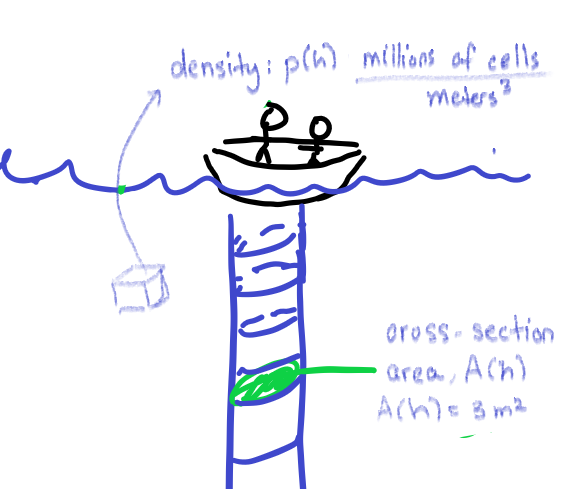
Figure 2: Another Sad Excuse of a drawing by Marizza
Step 3: Name Everything: Make sure you identify variables and relationships. Some are already given.
For h is in [0,30] ( units: h meters )
N(h) = number of plankton cells in column at h meters ( units: million cells )
![]() density of plankton
density of plankton
![]() of cross-section in column at h meters
of cross-section in column at h meters
Step 4: Determine math expressions from picture and math vocabulary units are very important in determining relationships.
We know that Volume = integral of area and that the area is constant and does not depend on the depth, but the plankton density does depend on the depth.
If we multiply, p(h) · A(h),the units are almost correct: ![]()
Step 5: Determine what you’re asked to find and solve Remember to use units to help you figure out what you need to solve.
They asked us for “how many plankton cells”, so we need units to be in millions of cells.
If we integrate p(h) · A(h), then we will be multiplying a dh to the equation: dh ( units: meters )
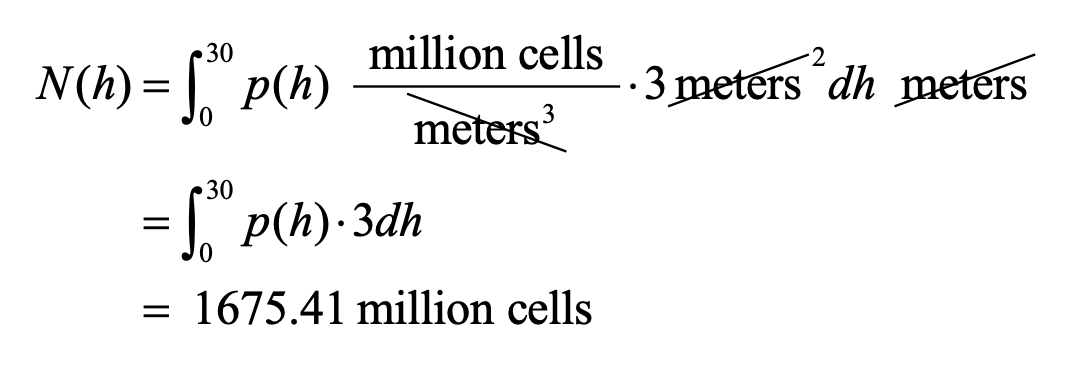
This is a calculator active question, so we can integrate using our calculator. They also asked us to round to the nearest million, so the answer is:
1675 million cells
The End
Of course, you can probably find some shortcuts, but this strategy is very useful when a word problem stumps you and you don’t know where to start.
So, remember, BREATHE … DON’T PANIC… and Underline, Draw, Name, Math, Find and Solve!
Now try the rest of the parts of this free response by following the link below:
https://apcentral.collegeboard.org/pdf/ap18-frq-calculus-bc.pdf?course=ap-calculus-bc
then you can check your answers by following the link below:
https://apcentral.collegeboard.org/pdf/ap18-frq-calculus-bc.pdf?course=ap-calculus-bc
Need help? Contact us here!
