As we move closer to the winter holidays, many students are earnestly preparing for mock exams – especially those readying themselves for GCSE or IGCSE. Revising for such a broad exam can be daunting, since there are many different topics to tackle. It’s always worth looking at past papers, since these can give you a good idea of where your weaknesses lie. It’s also worth doing some targeted revision, too, though, so in this blog post we’ve brought together some top hints and tips for a few bits of the GCSE and IGCSE specification that students often struggle with. This selection of questions are all related to scale factors, the multipliers that take you from one number to another. In general, we may write

You will usually find it more helpful when finding scale factors to rearrange this formula and to write:

or simply:

Don’t forget to read our other blogs about how best to revise for exams, The Revision Cycle and Revishun Revisoin Revision.

Joining ratios

I have a bag containing lots of sweets. The ratio of cherry sweets to raspberry sweets is 5 : 7. The ratio of raspberry sweets to strawberry sweets is 3 : 8. Find the ratio of cherry sweets to strawberry sweets.

The secret to this type of question lies in two things – common multiples and scale factors. The question is made clearer if you line all the information up neatly:

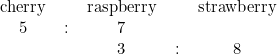
This would be much easier if the number of raspberry sweets on the first and second lines matched! This can be managed by scaling up each line of the table. The easiest way to do it is to find the lowest common multiple of 3 and 7, which is 21. By multiplying the top row by 3 and the bottom row by 7, the ratios can be written with a common middle term:

And so we can conclude that the ratio of cherry sweets to strawberry sweets is 15 : 56.

You can use this strategy when working with ratios with more parts, and no matter how big the numbers are – the most important thing is to line up the same components of each ratio vertically, so that you can see easily what common denominators to use.

Building walls and digging holes

This is another type of question where scale factors are the key. Questions typically read:

Ten workers can complete 40 assignments in 12 days. How long would it take 8 workers to complete 60 assignments, assuming that they work at the same rate?

There are lots of ways of tackling this kind of problem, but starting off with a table is a good way to begin:

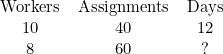
The first thing to do is identify the relationship between the known variables and the unknown variable. For example, if we increase the number of assignments, does it increase, or decrease the amount of time taken? And what about increasing the number of workers?

Hopefully, you’re satisfied that increasing the number of assignments will also increase the amount of time – so these two quantities are directly proportional. In contrast, if you increase the number of workers, the amount of time will be decreased – these quantities are inversely proportional. Where quantities are directly proportional, when one increases by a scale factor, so does the other. In this case, the scale factor increase in the number of assignments is

This means that the number of days will also be multiplied by a factor of  .

In contrast, when they are inversely proportional, this means that one decreases as the other increases. So the scale factor change in the number of workers is

This means that the number of days should be divided by , which is the same as multiplying by  .

Hence, the number of days needed is

Dealing with percentages

Scale factors are also the best way to deal with percentage problems. This is because the term “percent” – literally meaning “out of a hundred” naturally works well with division and multiplication. Consider the question:

Find 130% of 250.

The easiest approach is to identify that 130% means , and to recall that when we use the word “of” in mathematics, we often mean “multiply” (e.g. find 4 lots of 7 means ). Hence 130% of 250 is

Most other percentage problems can be dealt with in a similar way, provided you remember that the question needs to be structured as “Find …% of …”. What about this example?

Increase 400 by 27%.

The first step is to turn the “increase” instruction into a “find” instruction. Since the original quantity is always 100%, if we increase by 27% we are in fact finding 127%. So the question “Increase 400 by 27%” becomes

Find 127% of 400.

Which can be answered by doing

It’s just as easy to go the other way, and to decrease by a percentage.

Decrease £30,000 by 4%.

Decreasing the original 100% by 4% means finding 96%, or multiplying by 0.96. So “decrease £30,000 by 4%” really means

Find 96% of £30,000.

Which is

The good thing about this approach is that it makes it very easy to do reverse percentage problems, i.e. those where you are told a value or quantity after it has been adjusted. For instance

A coat is reduced in a sale by 7%. Its new price is $220.41. What was the original price?

Firstly, we note that reducing by 7% is the same thing as finding 93%, which corresponds to a scale factor of 0.93. So the original price multiplied by 0.93 gives $220.41. Therefore, the original price can be found by doing

Scale factors can also be used to answer questions about compound problems involving percentages:

What single percentage change is equivalent to increasing by 24% and then decreasing by 15%?

Now, if you thought the answer was “increasing by 9%”… read on! This is a common error.

Increasing by 24% is a scale factor of 1.24. Decreasing by 15% is a scale factor of 0.85. Doing both would require multiplying by both scale factors, or, alternatively, multiplying by their product. Since , so an increase of 5.4% – quite a long way off the common wrong answer of 9%. This is because when reducing by 15%, we are taking off 15% of the increased amount – not the original. Hence the amount removed is more than 15% of the original.

Try practicing these skills, along with all the others, using the practice questions below. And good luck with your revision!

Have a go!

The key to success is practice. So why not try embedding these techniques using the following questions?

Answers are below – don’t scroll too far!

1. I have a big bag of counters. The ratio of green to blue counters is 3 : 5 and the ratio of blue to yellow counters is 8 : 3. Find the ratio of green to blue counters.
2. Ed, Ned and Ted share a bag of sweets. Ed’s and Ned’s sweets are in the ratio 7 : 5. Ned’s and Ted’s sweets are in the ratio 11 : 12.
   What is the smallest number of sweets that the bag could contain?
3. Santa’s elves have made many toys this year. The ratio of dolls to cars is 12 : 7. The ratio of cars to teddies is 2 : 5, and the ratio of teddies to spinning tops is 6 : 5. In total, they make 217 more spinning tops than dolls.
   How many toys did they make in total?
4. Sixteen metres of material will make nativity play costumes for eleven toddlers. How many metres of fabric would I need to make similar costumes for eighteen toddlers?
5. 4 men take 3 days to dig a trench 48 metres long.
   How long will a second trench be, if it takes 6 men 5 days to dig?
6. I can feed three ponies for six days with four bags of oats. How many bags of oats would I need to feed eleven ponies for five days?
7. Three shop assistants can fold twenty Christmas jumpers in eight minutes. How long would it take two shop assistants to fold 25 Christmas jumpers, working at the same average rate?
8. Ten truculent troglodytes torture twenty-two terrified pterodactyls in twelve terms. How long would it take sixty similarly sadistic stone-age civilians to subject sixty-six of them to the same suffering?
9. What scale factor corresponds to:
   1. increasing by 20%?
   2. finding 30%?
   3. decreasing by 40%
10. What percentage change is the same as
    1. increasing by 30% and then increasing by 20%?
    2. increasing by 60% and then decreasing by 60%?
    3. decreasing by 20% and then increasing by 25%?
11. A year ago, my new headphones cost £150. Since then, the price increased by 8% and then by 6%. To the nearest pound, what is the cost of the headphones now?
12. Including sales tax of 7%, a new car costs $91,164.
    What is the price excluding sales tax?
13. A new games console is on sale. The shop is offering it for 15% off the ticket price. However, then add 5% sales tax to the ticket price.
    If the actual price I pay is $214.20, what was the ticket price for the console?

Answers

1. 8 : 5.
2. 192
3. 4291
4. 26.18 m
5. 72 m
6. 12.2 m
7. 15 minutes
8. 6 terms (or four semesters, if you prefer alliterative units!)
9. 1. 1.2; 2. 0.3; 3. 0.6
10. 1. 56% increase; 2. 36% decrease; 3. no change
11. £172
12. $85200
13. $240

Warp Drive Tutors, Inc. has been developed independently from and is not endorsed by Cambridge Assessment International Education. A-Level, GCSE and iGCSE are registered trademarks owned by Cambridge Assessment International Education.